Mathématiques
Le Scienteens Lab propose cinq ateliers de mathématiques pour les classes du secondaire. Ils portent sur la théorie des graphes, les probabilités, la cryptographie, la classification et la modélisation. La plupart de ces ateliers sont destinés aux élèves âgés de 16 à 19 ans. Ils se déroulent sur le campus de Belval, sous la supervision de l’équipe du Scienteens Lab. Chaque atelier est décrit ci-dessous. Vous pouvez également avoir un aperçu de ces ateliers grâce à une courte vidéo.
Cet atelier propose une introduction à la théorie des probabilités et présente aux élèves les concepts et les notions mathématiques sous-jacentes. Des exercices pratiques que les participants peuvent effectuer par eux-mêmes les aident à mieux comprendre comment aborder les calculs de probabilité. Au moyen d’exemples spécifiques, ils découvrent comment les concepts abordés peuvent aider à prendre une décision, par exemple dans le domaine de la médecine.
L’atelier couvre entre autres :
- des notions de base (expérience aléatoire, variable aléatoire, loi de probabilité)
- l’épreuve de Bernoulli et la loi binomiale
- la loi géométrique
- la probabilité conditionnelle
- des exemples et applications de la théorie des probabilités
Cet atelier est accessible à partir de la classe de 3e .
L’atelier est conçu pour être flexible et le rythme est adapté en fonction du niveau de chaque classe.
Il existe sous la forme d’une journée complète (6h30) ou d’une demi-journée (3-4h).
Pendant cet atelier, les élèves découvrent la théorie des graphes et apprennent comment différents concepts théoriques sont utilisés pour modéliser et résoudre des problèmes de la vie courante, par exemple dans la logistique et la planification d’itinéraire. Les élèves peuvent participer activement au travers de plusieurs exercices pratiques et ont l’opportunité de tester eux-mêmes les concepts présentés pendant l’atelier.
L’atelier aborde entre autres :
- le problème des sept ponts de Königsberg
- les graphes Eulériens et semi-Eulériens
- les graphes pondérés
- l’algorithme de Dijkstra pour trouver le chemin le plus court
- le problème du voyageur de commerce
- l’algorithme PageRank de Google
- des applications de la théorie des graphes dans la vie quotidienne
Cet atelier est accessible à partir de la classe de 4e.
Il existe sous la forme d’une journée complète (6h30) ou d’une demi-journée (3-4h).
Cet atelier de mathématiques permet aux lycéens de découvrir comment la théorie des nombres est utilisée pour sécuriser les communications. Au travers d’exercices pratiques, comme le décodage d’un message crypté avec une roue de décodage, les élèves découvrent comment fonctionne les algorithmes utilisés en cryptographie et la théorie des nombres sous-jacente.
Les élèves aborderont différents concepts mathématiques :
- la division euclidienne
- le plus grand diviseur commun (PGCD)
- l’algorithme d’Euclide étendu
- le petit théorème de Fermat
- l’algorithme RSA
Si les enseignants souhaitent préparer leurs classes avant l’atelier, du matériel pédagogique portant sur les notions importantes sera fourni. (voir l’onglet Prérequis pour plus de détails)
Cet atelier est accessible à partir de la classe de 3e .
L’atelier est conçu pour être flexible et le rythme est adapté en fonction du niveau de chaque classe.
Il existe uniquement sous la forme d’une journée complète (6h30).
Le concept de classification des objets, leur regroupement en différentes catégories selon certains critères, joue un rôle important dans de nombreuses sciences. En biologie, par exemple, les organismes vivants sont classifiés sur la base de caractéristiques communes et de leur histoire évolutive. En mathématiques, il en va de même et de nombreux mathématiciens s’intéressent à la classification des objets mathématiques.
Cet atelier présente le concept de classification et illustre son importance en mathématiques. À l’aide d’exemples tels que les nombres, les graphes ou les formes géométriques, les élèves découvrent comment les objets mathématiques peuvent être classifiés et apprennent comment utiliser certaines propriétés dites invariantes pour distinguer les objets.
Cet atelier convient aux élèves à partir de la 3e.
Il existe uniquement sous la forme d’une demi-journée (3-4h).
Cet atelier donne aux élèves un aperçu de la modélisation mathématique et leur montre comment des problèmes réels peuvent être modélisés et résolus grâce aux mathématiques. Il est divisé en deux parties.
Au cours de la première partie, les élèves apprennent comment formuler un problème d’optimisation linéaire et comment un problème à deux variables peut être résolu graphiquement. Ils découvrent ensuite l’algorithme du simplexe qui peut être utilisé lorsqu’il y a plus de deux variables.
La deuxième partie est consacrée à la modélisation des processus de croissance et traite en particulier le modèle SIR qui permet de modéliser la propagation d’une épidémie dans une population donnée.
L’atelier aborde entre autres :
- des exemples de problèmes d’optimisation linéaire
- la résolution graphique d’un problème à deux variables (à l’aide de GeoGebra)
- l’algorithme du simplexe
- la croissance linéaire, exponentielle et logistique
- le modèle SIR et son implémentation dans GeoGebra
Cet atelier est accessible à partir de la classe de 3e.
Il existe sous la forme d’une journée complète (6h30) ou d’une demi-journée (3-4h).
Les classes qui viennent pour une demi-journée doivent choisir entre les deux parties de l’atelier (optimisation ou dynamique des populations).
Pour la partie sur l’algorithme du simplexe, il est utile que les élèves aient déjà des connaissances sur les systèmes d’équations linéaires.


Informations pratiques pour tous les ateliers de mathématiques
Tous les ateliers de mathématique sont destinés à des classes allant de la 3e à la 1ère (niveaux du système scolaire luxembourgeois), c’est-à-dire des élèves âgés de 16 à 19 ans.
L’atelier 2 (théorie des graphes) peut aussi convenir aux classes de 4e .
Les ateliers de mathématiques se déroulent en luxembourgeois, français, allemand ou anglais.
Les ateliers 1, 2 et 5 (Lois de probabilités, Théorie de graphes et Modélisation) existent sous la forme d’une journée complète (6h30) ou d’une demi-journée (3-4h). L’atelier 3 (Théorie des nombres) existe uniquement sous la forme d’une journée complète (6h30). L’atelier 4 (Classification) existe uniquement sous la forme d’une demi-journée (3-4h).
Les ateliers sur la journée se déroulent de 9h à 15h30 avec une pause déjeuner d’une heure. Pendant la pause déjeuner, les élèves peuvent manger au restaurant universitaire ou dans les restaurants situés sur le campus et dans Belval Plaza. Les horaires de la pause repas doivent être respectés afin que les activités de l’après-midi puissent reprendre à l’heure.
Les classes qui viennent pour une demi-journée peuvent choisir l’heure de démarrage qui leur convient le mieux (choix effectué au moment de l’inscription).
Les ateliers de mathématiques se déroulent à la Maison du Savoir sur le Campus Belval.
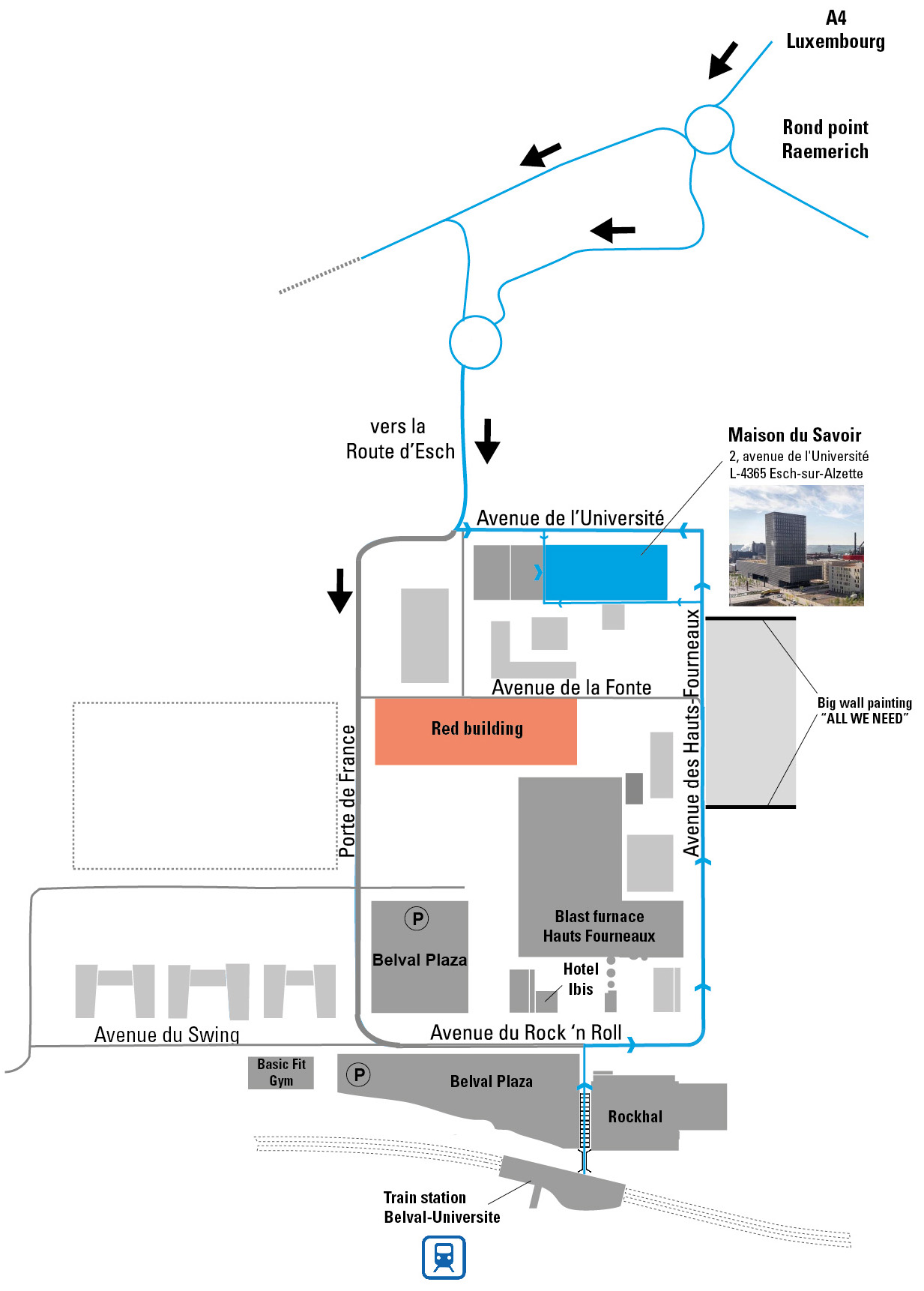
Si vous venez en voiture ou en car, prenez l’A4 et suivez-la jusqu’au bout, puis suivez les panneaux vers « Belval ». Sur le campus, il n’y a malheureusement aucun panneau indiquant le chemin jusqu’au bâtiment de la Maison du Savoir. Veuillez utiliser le plan ci-dessous pour vous y rendre.
Si vous venez en train, descendez à la gare de « Belval Université ». Notre bâtiment se trouve à environ 10 minutes de marche de la gare. Plusieurs bus peuvent également vous amener jusqu’au Campus de Belval.
Pour l’atelier 3 (Garder un secret ? Grâce à la théorie des nombres !), si vous souhaitez préparer la classe avant l’atelier, vous pouvez rappeler ou introduire les notions suivantes :
a) Division euclidienne (division avec reste) et algorithme d’Euclide (pour la division, aussi voir les cas avec un dividende/diviseur négatif).
b) Le plus grand diviseur commun (PGCD) de 2 nombres entiers et le théorème de Bachet-Bézout qui donne le plus grand diviseur commun de 2 nombres entiers comme une combinaison linéaire.
Par exemple 3 = pgcd(6, 15) = -12*6 + 5*15. Une telle combinaison linéaire peut être obtenue avec l’algorithme d’Euclide étendu.
c) Définition d’un nombre premier.
d) Les règles de base de l’exponentiation.
Du matériel pédagogique portant sur ces notions sera fourni aux enseignants.
À la fin d’un atelier, chaque élève reçoit un certificat attestant de sa participation.